MHD

Les équations de base de la MHD (partie hydrodynamique)

• Il est possible de les établir à partir d’équations bi-fluides, elles mêmes obtenues à partir d’équations de Boltzmann (voir article de revue de J.P. Friedberg). Une autre façon (plus intuitive) est de les établir directement à partir de règles de conservation d’un fluide conducteur (voir ci-dessous).

• Equation de base pour la conservation d’une quantité physique scalaire $F$ dont la densité par unité de volume est $f$: elle s’écrit, $\frac {\partial f} {\partial t} + \nabla . (f \vec V) = s$. En effet, elle exprime que dans un petit volume fixe, $f$ varie dans le temps (premier terme) à cause des entrées/sorties du fait du flot de vitesse par la surface enfermant ce volume (second terme), et aussi à cause de création/disparition en volume exprimée par le terme $s$ qui est un taux de création en volume. Ceci se démontre facilement en utilisant le théorème de Gauss-Ostrogradsky (dit aussi de la divergence), pour le terme de divergence du flux $f \vec V$.

• Equation de conservation de la masse, dite aussi équation de continuité. Celle ci est obtenue en appliquant la règle ci-dessus avec $f = \rho$ et en considérant $s = 0$ (pas de création ni de disparition de masse par exemple par réaction chimique). Le terme $ (\rho \vec V)$ représente ainsi le flux de masse.
  • Equation 1: \(\boxed{\frac {\partial \rho} {\partial t} + \nabla . (\rho \vec V) = 0}\)
• Equation de conservation de la quantité de mouvement. Celle ci est la plus importante pour la dynamique (équivalent de la seconde loi de Newton qui exprime que la densité de quantité de mouvement $(\rho \vec V)$ varie du fait d’un flux convectif associé, et aussi de création/disparition du fait des densité de forces). Celle ci se démontre en appliquant la règle pour chaque composante de $(\rho \vec V)$, et fait apparaître un tenseur de rang 2 (terme $\overline{\overline {V \rho V }}$) pour le flux associé, et les termes sources qui sont toutes les densités de force s’appliquant en volume sur le plasma (termes de gradient de pression thermique, de force magnétique de Lorentz, et de force visqueuse). Le coefficient $\mu$ est la viscosité dynamique ou le coefficient de dissipation visqueuse (unité SI en kg m^{-1} s^{-1}). Parfois, il faut aussi ajouter d’autres densités de force comme la force de gravitation lorsque c’est nécessaire, suivant le milieu considéré.
  • Equation 2: \(\boxed{\frac {\partial (\rho \vec V)} {\partial t} + \nabla . ( \overline{\overline {V \rho V }} ) = - \nabla P + \vec J \times \vec B + \mu \nabla^2 \vec V}\)
  • Il faut noter que la composante $i = x, y, z$ (en cartesien) de $\nabla . ( \overline{\overline {V \rho V }} )$ est $\nabla_j (V_j \rho V_i )$, avec la convention habituelle de somme implicite sur les indices répétés (ici sur l’indice $j$). Il n’y a pas de densité de force électrique à cause de l’hypothèse de quasi-neutralité (voir la partie électromagnétique des équations MHD plus bas dans cette page).
• Equation de conservation de l’énergie. Plusieurs équations sont possibles suivant les hypothèses d’échanges entre les différentes formes d’énergie: énergie cinétique, énergie interne, et énergie électromagnétique. Ici, on considère un exemple simple d’une évolution de type adiabatique conduisant alors à une équation de conservation pour l’énergie interne $u$ du plasma.
  • Equation 3: \(\boxed{\frac {\partial u} {\partial t} + \nabla . ((u+ P) \vec V) = \vec V . \nabla P }\)
  • On notera que le flux associé est maintenant $ (u+ P) \vec V$ (car c’est le flux d’enthalpie qu’il faut considérer), et que le terme source provient du travail des forces de pression (provenant d’un échange avec l’énergie cinétique du plasma).
  • Il manque une équation pour fermer le système (terme employé habituellement dans la litérature) qui est en général l’équation d’état du plasma qui est supposé parfait (à l’image d’un gaz parfait), ainsi on écrit $P = \alpha \rho T$ conduisant à \(\boxed{u = P/ (\Gamma - 1)}\) ($\Gamma$ étant la constante adiabatique). Ainsi, une autre forme équivalente pour l’équation ci-dessus est,
  • Equation 3b: \(\boxed{\frac {\partial P} {\partial t} + \vec V . \nabla P = - \Gamma P \nabla . \vec V }\)
• La seconde équation ci-dessus peut aussi sous une autre forme équivalente (obtenue en utilisant la première équation):
  • Equation 2b: \(\boxed{\frac {\partial \vec V} {\partial t} + (\vec V . \nabla) \vec V = (- \nabla P + \vec J \times \vec B)/\rho + \nu \nabla^2 \vec V}\). Cette forme fait apparaitre dans le membre de gauche la dérivée Lagrangienne (ou encore appelée dérivée en suivant le fluide car c’est la dérivée dans un repère se déplaçant avec le fluide à la vitesse $\vec V$. On note le coefficient de viscosité cinématique $\nu = \mu / \rho$ (unité SI en $m^2/s$). Cette équation en l’absence du terme de force magnétique (cas purement hydrodynamique) est en fait l’équation bien connue de Navier-Stokes.

Les équations de base de la MHD (partie électromagnétique)

• La première équation de Maxwell (dans l’approximation du vide) est celle de Maxwell-Gauss qui relie le champ électrique $\vec E$ à la densité volumique de charge $\rho_c$ en chaque point de l’espace: $\nabla . \vec E = \rho_c/\epsilon_0$. Pour un plasma de type fluide, dont la description est valide sur des échelles spatiales plus grandes que les échelles caractéristiques des particules, la densité de charge est considérée comme nulle (c’est la quasi-neutralité) conduisant ainsi à la première équation:
  • Equation 1E: \(\boxed{\nabla . \vec E = 0}\)
• La seconde équation est celle Maxwell-Ampère qui relie le champ magnétique $\vec B$ à la densité de courant $\vec J$: $\nabla \times \vec B = \mu_0 \vec J + \mu_0 \epsilon_0 \frac {\partial \vec E} {\partial t}$. Le second terme appelé courant de déplacement est négligeable si on s’intéresse à des vitesses caractéristiques de plasma très inférieures à la vitesse de la lumière, conduisant ainsi à la seconde équation relevante pour la MHD:
  • Equation 2E: \(\boxed{\nabla \times \vec B = \mu_0 \vec J}\)
• La troisième équation est celle de Maxwell-Faraday (rendant compte des phénomènes d’induction),
  • Equation 3E: \(\boxed{\nabla \times \vec E = - \frac {\partial \vec B} {\partial t} }\)
• La quatrième équation exprime tout simplement la propriété de divergence nulle (dite aussi propriété solénoïdale) du champ magnétique,
  • Equation 4E: \(\boxed{\nabla . \vec B = 0}\)

Couplage partie électromagnétique & partie hydrodynamique

• La densité de courant électrique $\vec J$ et le champ magnétique $\vec B$ interviennent dans la partie hydrodynamique (Equation 2) au travers de la densité de force magnétique $\vec J \times \vec B$, c’est la rétro-action de la partie électromagnétique sur partie hydrodynamique. Cependant, il manque la rétro-action inverse, celle de la partie hydrodynamique sur la partie électromagnétique. Celle ci résulte de la loi d’Ohm, qui exprime que la densité de courant est proportionnelle au champ électrique $\vec E$ augmenté d’un champ électrique $V \times \vec B$ d’un milieu animé d’une vitesse $\vec V$,
  • Loi d’Ohm: $\vec J = \sigma (\vec E + \vec V \times \vec B) $ ($\sigma$ étant la conductivité électrique)
• Ce qui peut se résumer en combinant la loi d’ohm avec l’équation de Maxwell-Faraday en,
  • \(\boxed{\frac{\partial \vec{B}} {\partial t} = \nabla \times (\vec{V} \times \vec{B}) - \nabla \times (\vec{J}/\sigma)}\),
  • et plus précisément pour une conductivité uniforme (en posant $\eta = 1/(\mu_0 \eta)$,$ \frac{\partial \vec{B}} {\partial t} = \nabla \times (\vec{V} \times \vec{B}) + \eta \nabla^2 \vec{B}$

A quoi peut servir la MHD ?

• Elle est utile pour calculer des équilibres statiques. Les équilibres MHD statiques (ou du moins des configurations proches) sont réalisés dans la couronne solaire en dehors des période d’activité intense et/ou de régions actives (donnant des éruptions). C’est aussi le cas dans les machines à fusion magnétique prinicpalement en dehors des instabilités. Ainsi, on peut espérer que les flots de vitesse tendent vers zéro. De plus la dissipation étant faible, on se ramène alors à chercher des solutions de l’équation,
  • \(\boxed{ - \nabla P + \vec J \times \vec B = 0}\), assortie de conditions aux limites du domaine spatial considéré pouvant êtres vues comme des contraintes sur la solution (ou plutôt sur l’espace des solutions possibles).
• Les solutions générales obéissent quand même à certaines propriétés. En effet, on peut tout d’abord montrer que le vecteur champ magnétique $\vec B$ ainsi que le vecteur densité de courant $\vec J$ appartiennent à des surfaces (appelées surfaces magnétiques) sur lesquelles la pression thermique $P$ est constante (découle de $\nabla P . \vec B = 0$ et de $\nabla P . \vec J = 0$). Ainsi, les lignes de champ du champ et du courant s’enroulent sur ces surfaces en faisant un certain angle non nul (sauf si le gradient de pression est nul), comme représenté sur la figure ci-dessous pour des surfaces de type toriques emboîtées les unes dans les autres. Bien sûr, on considère des équilibres non stochastiques avec des lignes de champ bien définies, sinon l’équilibre est plus délicat à définir.
  • Dans le cas de la couronne solaire, le gradient de pression thermique est négligeable conduisant alors aux équilibres dits ‘force-free’ (ou sans force) avec, $\vec J = \alpha \vec B$, où $\alpha$ est fonction de l’espace (le cas $\alpha = cste$ étant un cas particulier dit linéaire sans force). Un autre cas dit ‘current-free’ (ou sans courant) est parfois aussi envisagé car $\vec J$ est nul. Dans ce dernier cas, celà ne signifie pas qu’il n’y a pas de champ magnétique, car celui ci peut être bien sûr créé par une source de courant éloignée de la structure.

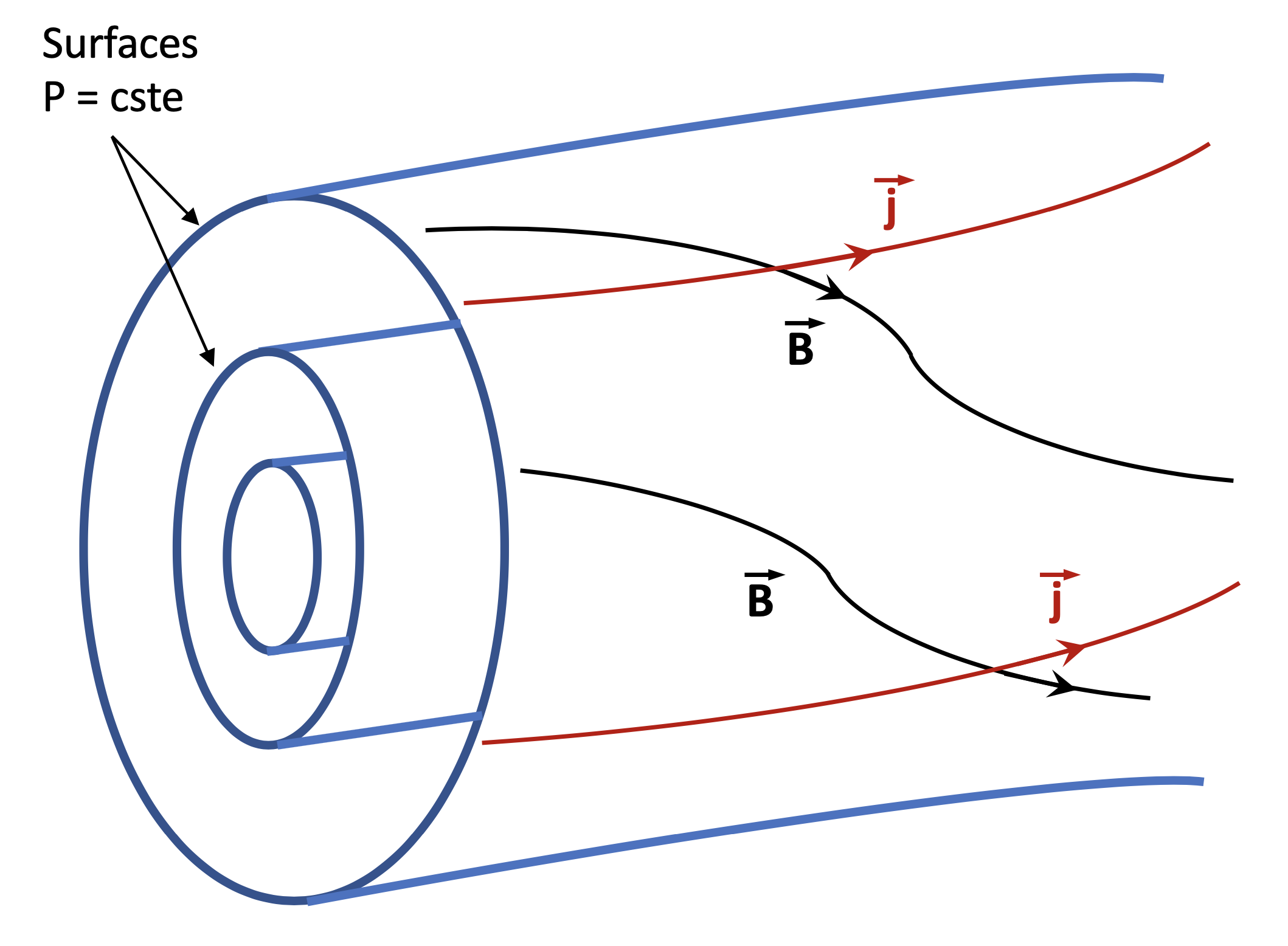
(Figure schématique d’un équilibre MHD statique)

• La MHD sert aussi à modéliser des instabilités se développant sur des échelles macroscopiques (grandes devant les échelles spatiales caractéristiques associées aux particules du plasma), ainsi que le mécanisme de reconnexion magnétique associé (voir autres pages de ce blog et notamment ma recherche).

Instabilités magnétohydrodynamiques et reconnexion magnétique

• Un document/ouvrage est disponible sur HAL -> https://hal.archives-ouvertes.fr/hal-03711796