Plasma
C’est quoi un plasma ?
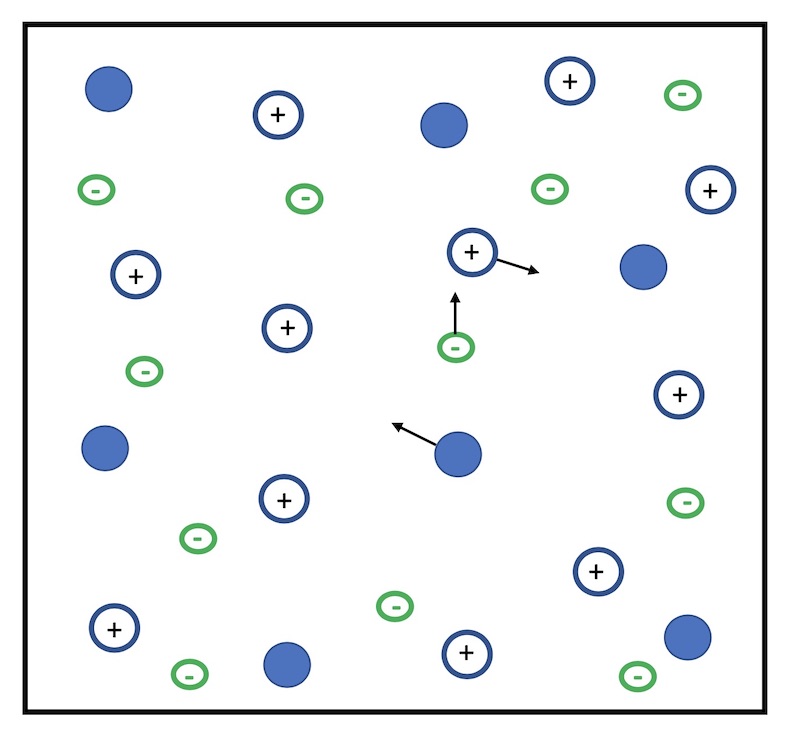
- Un plasma est un milieu contenant des ions (chargés positivement car issus d’atomes ou molécules ayant perdu un ou plusieurs électrons), des électrons libres, et des atomes ou molécules neutres. Les ions peuvent être multi-chargés. C’est un milieu globalement neutre (charge totale nulle). Le schéma ci-dessus illustre le cas d’un plasma mono-chargé (un ion est constitué d’un seul proton). Chaque type de particule est animé d’une vitesse moyenne d’agitation thermique qui dépend la sa température et de sa masse (comme pour un gaz).
- Un plasma (considéré comme le quatrième état de la matière) peut être obtenu en portant un gaz (atomique ou moléculaire) donné à une température supérieure à une valeur critique qui dépend de la composition. Ainsi, ceci permet d’ioniser le gaz par ‘arrachement’ des électrons. La température critique est de l’ordre de quelques électrons-volts en moyenne (en terme d’énergie thermique $k_BT$, $k_B$ étant la constante de Boltzmann), ou encore de façon équivalente de plusieurs dizaines de milliers de degrés Kelvin pour $T$. Cependant, certains plasmas peuvent exister à des températures beaucoup plus basses (quelques centaines de degrés) à cause de densités extrêmement faibles de certains milieux astrophysiques (voir schéma plus bas).
- L’ionisation est plus ou moins forte selon que le nombre restant d’atomes (ou molécules) neutres est plus ou moins grand. En pratique, on parle de degré d’ionisation $\alpha$ plus ou moins proche de l’unité. Celui ci est défini de la façon suivante, $\alpha = \frac{n_e}{n_e+n_n}$ avec $n_e$ la densité électronique et $n_n$ la densité de neutres. Un plasma complètement ionisé correspond ainsi à $\alpha = 1$. Les modèles décrits ci-dessous concernent essentiellement des plasmas dont l’ionisation est suffisament grande pour que la dynamique de la population des particules neutres soit considérée comme négligeable.
- L’ionisation peut-être aussi obtenue d’une autre façon comme par décharge électrique dans un gaz, ou encore par rayonnement (cas des régions de formation d’étoiles).
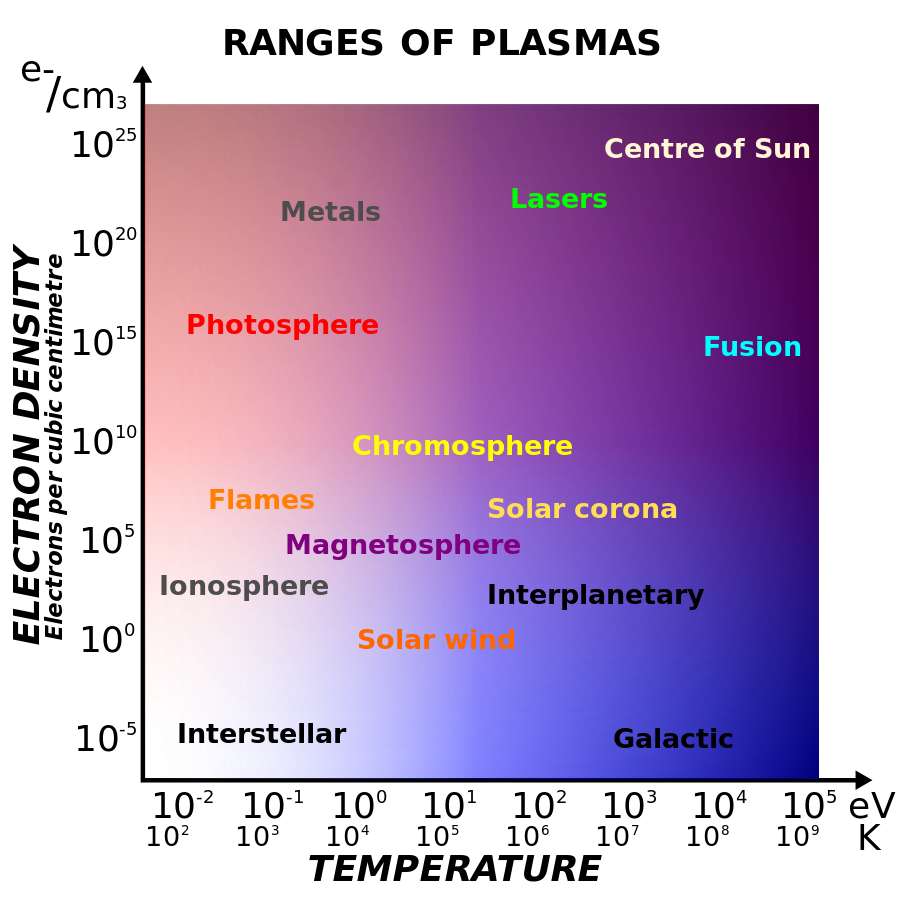
(Figure tirée de Wikipédia)
Exemples de plasmas
- En astrophysique de nombreux objets astronomiques comme les étoiles (l’intérieur comme leur couronne), les disques d’accrétion, les nébuleuses, et le milieu interstellaire sont composés de plasma. On peut aussi ajouter les milieux entourant l’atmosphère de la Terre comme l’ionosphère ou de façon plus lointaine la magnetosphère. On parle alors de plasmas naturels, par opposé aux plasmas de laboratoires (comme par exemple ceux créés dans le but de réaliser la fusion thermonucléaire). Sur la figure ci-dessus, chacun peut constater la diversité impressionnante de conditions, en termes de température et de densité, régnant au sein de différents plasmas.
- On s’intéresse ici à des plasmas classiques, c’est dire non-relativistes et non quantiques. De plus, on exclut aussi les plasmas dit fortement couplés comme les plasmas froids, pour se focaliser sur les plasmas dilués.
Modèles de description des plasmas
Il existe un grand nombre de modèles physiques permettant de décrire la dynamique des plasmas. Le lecteur pourra trouver ci-dessous un résumé simplifié et très succint. Le modèle MHD sera évidemment plus amplement développé (voir l’onglet correspondant).
- Les modèles PIC (abréviation pour ‘Particle In Cell’)
- Ils sont basés sur l’intégration numérique de l’équation du mouvement (seconde loi de Newton de la dynamique) pour chaque particule chargée (de charge $q$ et masse $m$), soumise à la force électique $q \vec E$ et la force magnétique $q (\vec V \times \vec B)$. Ainsi, un très grand nombre de particules (représentant les ions et électrons) sont implémentés avec un pas de temps $\delta t$ par une technique numérique adaptée dans les champs électrique et magnétiques $\vec E$ et $\vec B$ respectivement. La méthode numérique doit ainsi satisfaire des propriétés particulières de conservation (comme celle de l’énergie), comme par exemple dans les schémas de type Boris. A la fin de cette première étape, la position ainsi que la vitesse de chaque particule sont ainsi déduites.
- Une fois les particules implémentées, dans une seconde étape, il faut calculer les champs $\vec E$ et $\vec B$ correspondants à la ‘nouvelle’ distribution des particules dans l’espace des phases (c’est à dire l’espace physique et l’espace des vitesses). Pour ce faire, il faut intégrer par rapport à l’espace les équations de Maxwell correspondantes dans l’approximation du vide, que sont l’équation de Maxwell-Gauss (pour $\vec E$) et l’équation de Maxwell-Ampère (pour $\vec B$). Ceci est alors réalisé sur un domaine découpé en cellules, et nécéssite un lissage pour éviter les gradients trop irréalistes de distribution des particules.
- Les limitations de la méthode sont multiples. Tout d’abord le nombre maximum de particules est évidemment très inférieur à la réalité, et on parle alors de super-particules. Le rapport de masse entre les ions et les électrons limite fortement le temps de calcul au travers des conditions de stabilité des schémas numériques, conduisant ainsi à l’emploi d’un rapport de masse moins grand dans les simulations.
- Malgré les limitations, ces modèles permettent une approche complémentaire des modèles cinétiques et fluides (voir ci-dessous). Ils constituent aussi une approche naive et beaucoup plus simple techniquement que les autres modèles.
- Les modèles dits cinétiques
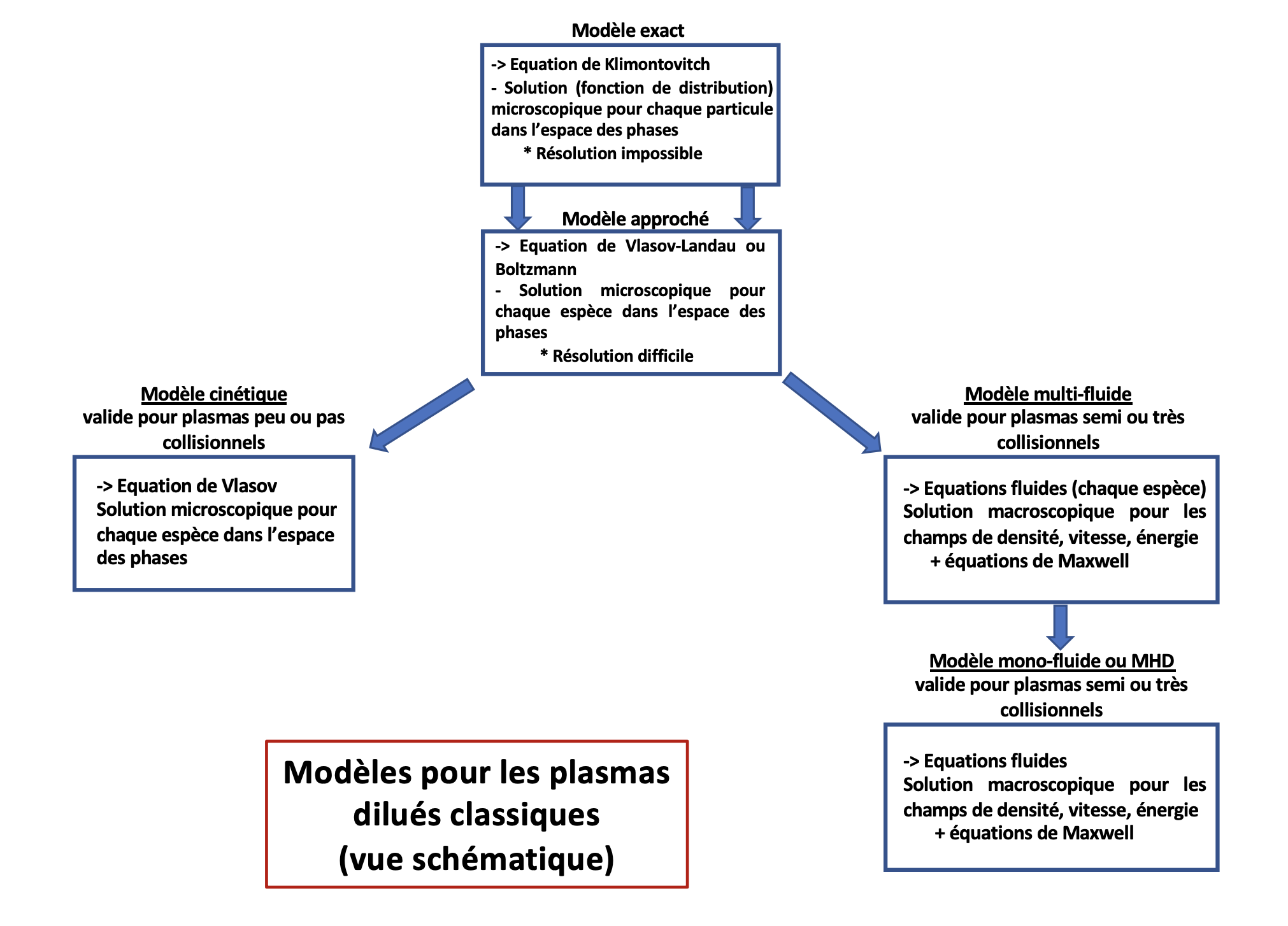
- Ils sont utilisés lorsque le plasma étudié est dit non (ou peu) collisionnel, car les collisions sont peu fréquentes et donc influent peu le mouvement des particules (voir schéma ci-dessous). Il s’agit de résoudre une équation de type Vlasov (avec ou sans opérateur tenant compte d’un minimum de collisions). Ce type de modèle est considéré comme un modèle approché du modèle exact (équation de Klimontovitch ou approche statistique de Liouville). En effet, au lieu de résoudre le comportement microscopique de chaque particule (ce qui est évidemment impossible) dans l’espace des phases, on cherche la fonction de distribution par espèce $f (\vec r, \vec V, t)$ (électrons ou ions) qui résulte d’une moyenne d’ensemble statistique et qui est donc solution de l’équation de Vlasov-Landau (aussi appelée équation de type Boltzmann dans la littérature). Le passage rigoureux du modèle de Klimontovitch à l’équation de Vlasov-Landau constitue une étape relativement complexe en théorie des plasmas, mais il permet d’obtenir des solutions approchées au prix d’une perte d’information sur la physique individuelle des particules.
- Equation de Vlasov (sans collisions) pour une espèce de particules (électrons ou ions de masse $m$ et charge $q$): $ \frac {\partial f} {\partial t} + \vec V . \frac {\partial f} {\partial \vec r} + (q/m) (\vec E + \vec V \times \vec B) . \frac {\partial f} {\partial \vec V} = 0$. Il ne faut pas confondre avec l’équation de Klimontovitch qui prend une forme similaire, mais pour laquelle la fonction de distribution doit être remplacée par une fonction individuelle associée à chaque particule (et les champs électromagnétiques ne sont plus moyennés).
- Les modèles dits fluides
- Ces derniers sont utilisés lorsque le plasma étudié est suffisament dominé par les collisions. Les modèles se ramènent alors à résoudre des équations de type fluide pour chaque espèce couplées aux équations de Maxwell pour les champs électromagnétiques, et on parle alors de modèle multi-fluide. Le modèle particulier dit mono-fluide pour lequel le plasma est vu comme un seul fluide conducteur est appelé Magnétohydrodynamique (ou MHD). Ainsi, le plasma est caractérisé par des champs de type densité, vitesse, énergie cinétique, … reliés aux paramètres physiques des particules par des intégrales sur les fonctions de distribution $f (\vec r, \vec V, t)$ (solutions de l’équation de Vlasov-Landau). Plus précisément, on utilise les moments d’ordre croissant sur les fonctions de distribution pour définir les champs et obtenir les équations différentielles associées. Pour l’exprimer autrement, on accepte de perdre de l’information sur la partie vitesse de l’espace des phases pour les distributions des électrons et des ions. Cette perte d’informations est évidemment plus ou moins acceptable suivant les plasmas considérés (voir plus bas les conditions de validité d’un modèle fluide et les implications en terme d’échelles spatiales et temporelles).
- En résumé, la MHD est constituée d’un premier jeu de trois équations différentielles de conservation permettant de calculer la densité volumique du plasma $\rho$, la vitesse $\vec V$ (à ne pas confondre avec la vitesse des particules), et la température $T$. Une hypothèse d’équation d’état est aussi nécéssaire pour relier $T$ et $\rho$ à la pression thermique $P$ (relation dite de fermeture) intervenant par exemple dans l’équation de conservation de la quantité de mouvement. Une équation différentielle supplémentaire (déduite des équations de Maxwell et de la loi d’Ohm) permet aussi d’obtenir le champ magnétique $\vec B$.
La MHD
- Le modèle MHD (équations, obtention, hypothèses) est décrit en détails sur la page correspondante. Cependant, le passage d’un modèle bi-fluide à un modèle mono-fluide mérite ici quelques explications. Tout d’abord, la densité volumique du plasma $\rho (\vec r, t)$ représente essentiellement celles des ions, car la masse des électrons est négligeable. De même, la vitesse de plasma $\vec V (\vec r, t)$ représente celle des ions. La vitesse des électrons (qui n’est pas un paramètre du modèle MHD) peut alors s’en déduire à condition de connaître la densité de courant électrique $\vec J$, par $\vec V_e = \vec V - \vec J /(ne)$, avec $n$ la densité de particules (on suppose $n_e = n_i$ qui est l’hypothèse de quasineutralité de la MHD, et $e$ étant la charge électronique). La densité de courant est elle obtenue en résolvant les équations de Maxwell.
- La MHD est évidemment aussi le modèle permettant de décrire la dynamique des fluides réels (pas seulement de certains plasmas) conducteurs de l’électricité.
- Une autre façon d’obtenir les équations MHD est de les établir directement par l’utilisation de bilans de conservation appliqués à la masse, quantité de mouvement, et énergie, pour un petit volume fixe (appelé globule) de plasma. Il faut bien sûr ajouter les équations de Maxwell appliqués à des champs moyens. Ceci est développé quelque peu dans l’onglet MHD.
Quelques références
- Physique des plasmas, J.L. Delcroix et A. Bers, EDPsciences
- Un site très sympa et très bien écrit (notions sur les plasmas) -> http://www.mmelzani.fr
- Sur les modèles et la MHD -> ‘Ideal MHD’, J.P. Friedberg. Voir aussi ‘Ideal magnetohydrodynamic theory of magnetic fusion systems’, J.P. Friedberg, Rev. Mod. Phys. 54, 801 – Published 1 July 1982 (https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.54.801)
